有機反応の回帰分析 - 分子場解析入門

本サイトでは分子場解析のノウハウの公開を中心に有機合成化学者が自力でデータ解析研究を立ち上げ論文化するために役立つ情報を提供していきます。論文を書くためには当たり前ですが、有機化学におけるデータ科学の背景知識が必須になります。本サイトではデータ科学のなかでもとくに少数サンプルを用いた回帰分析に焦点をあてていきます。有機反応の少数サンプルの回帰分析といえばHammett則です。有機反応の回帰分析の原点はHammett則であると考えています。つまり有機反応のデータ解析に関する筆者の基本的な考え方は以下になります。

分子記述子を用いた少数サンプルの回帰分析はHammett則の拡張である

有機化学における回帰に基づくデータサイエンスの背景として、Hammett則とその拡張について見ていきます。

Hammett則

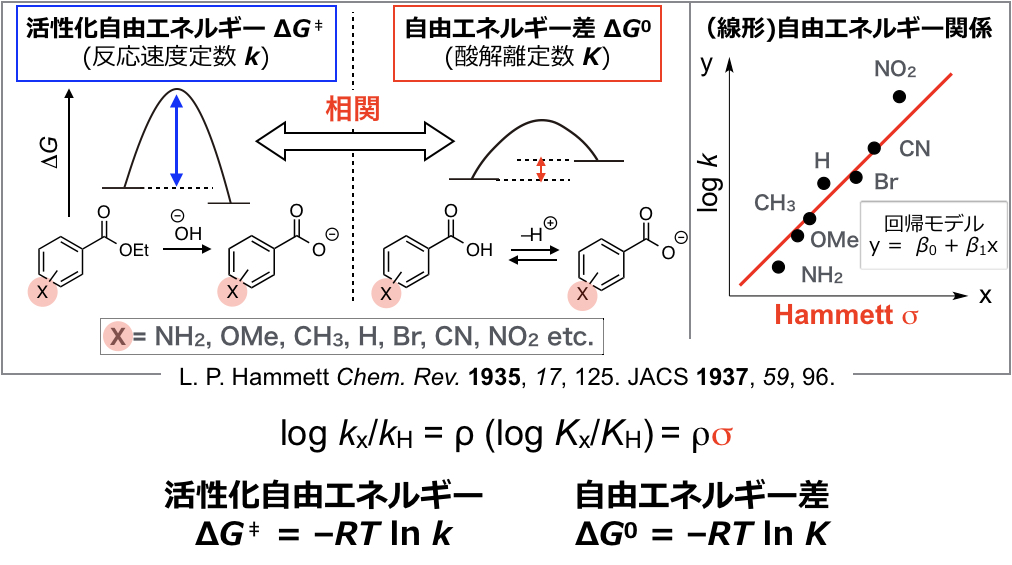
1930年代、Hammettは、上図にそのイメージを示すようにパラおよびメタ位に種々の置換基を持つ安息香酸エステルの加水分解における反応速度定数の対数と、対応する置換安息香酸の酸解離定数の対数との間に以下のような直線関係が成り立つことを見出しました。（k_x、K_xはそれぞれ置換基Xをもつ安息香酸エステルの加水分解反応速度定数および安息香酸の酸解離定数）

log k_x/k_H = ρ(log K_x/K_H) = ρσ

安息香酸の酸解離定数より計算されるこのHammett σは現在でも様々な有機反応の回帰分析のための記述子として使われています。上図に示したように、反応速度定数の対数は活性化自由ネルギーに、安息香酸の酸解離定数は酸解離前後の自由エネルギー差に対応するため、Hammett則は（線形）自由エネルギー関係（Linear Free Energy Relationships）と呼ばれます。後述する定量的構造活性相関分野の父ともいえるHanschらが書いた”Exploring QSAR“という本によると、当時の研究者からは、自由エネルギー差から反応の活性化エネルギーを予測できることは大変驚かれたようです。

“安息香酸とフェニル酢酸類のイオン化の平衡定数が直線関係にあることは、特に意外なことでない。Hammettと同時代の研究者が驚いたのは、Hammettの関係が速度定数でも成立することであった。(Hansch et al. Exploring QSAR 1995)”

Hammett則の拡張研究は物理有機化学の重要な一分野を築いています。Hammett σは分子の電子的性質をあらわす記述子ですが、たとえば立体効果を表す記述子として、Taftは酸性条件下での脂肪族エステルの加水分解速度定数から算出されるTaft E_sを考案しています(R. W. Taft, JACS 1952, 74, 2729; JACS 1952, 74, 3120; JACS 1953, 75, 4538.)。

1960年代に入るとHammett σやTaft E_sなどの記述子を用いることで回帰により生物活性が予測できることがHansch、藤田らにより報告されました(Nature 1962, 194, 178; JACS 1964, 86, 1616.)。今日では分子記述子を用いた生物活性の回帰による予測は定量的構造活性相関（QSAR: Quantitative Structure-Activity Relationships）として知られており、ケモインフォマティクスの重要な一分野を築いています（分子記述子を用いた生物活性以外の分子の性質予測はQSPR [Quantitative Structure-Property Relationships]と呼ばれます。）。

非常にざっくりとした紹介となりますが、上記が筆者が踏まえておくべきと考える有機化学の回帰分析の背景の大筋となります。より詳細な話を知りたい場合は上述したHanschらの”Exploring QSAR“を読むのがオススメです。とくにHammett則等を紹介しているはじめの数章は有機反応の回帰分析に取り組む研究者にとって必読だと思います。2000年以前にかかれたこの本の、はじめの数章に登場する記述子には、多少かたちを変えていますが、いまでも有機反応の回帰分析において第一線で活躍しているものも少なくありません。本サイトで後々ご紹介する分子場解析も、この本で紹介されています。反応のデータ解析分野の奥深さの一端に触れられる本かと思います。

さて、QSARが出てきましたので、アメリカ化学会のケモインフォマティクスの専門誌、J. Chem. Inf. Model.に掲載された”Understanding the Roles of the “Two QSARs”“というPerspectiveをご紹介したいと思います。というのも、このPerspectiveは有機低分子を用いた回帰分析研究を行う上で非常に重要な概念を述べていると考えているからです。その概念とは以下になります。

QSAR/QSPRの目的には現象の"解釈"と"予測"の2通りがある。

より具体的に書けば、上記PerspectiveによるとQSAR/QSPRは以下の2つに大別されます。

Extra-thermodynamic relationships within small sets of chemically similar molecules focused on mechanistic interpretation.
(少数の類似した化合物を用いた結果の解釈のためのQSAR/QSPRモデル)
(Model) that relies on machine learning methods to generate models from large, chemically diverse data sets for predictive purposes.
(大量かつ多様な化合物の機械学習に基づく予測のためのQSAR/QSPRモデル)

前者にはHammett則といった自由エネルギー関係が含まれます。本サイトでこれから見ていくようにHammett則や関連する回帰分析では作成した回帰モデルの回帰係数等をもとに反応機構に関する解釈を行うことを主目的としています。反応機構に関する情報が得られるものの、予測範囲が狭いという特徴を持ちます。

後者は深層学習に代表される機械学習手法を活用し、大量の訓練データから生物活性といった分子の性質を予測することを目的としています。予測可能範囲は広いものの、なぜ予測できてるかはわからないことが多い、つまり現象の解釈は難しいことが多いのが特徴です。分子設計を行う場合はハイスループットバーチャルスクリーニングやベイズ最適化などを用いて、作成した関数空間を効率的に探索することで所望の性質を持つ分子を探しだします（いわゆる逆解析。イメージとしてはこの総説のFigure 2がわかりやすいです）。

私自身はブラックボックスでの予測は好きではなく、前者の解釈のためのデータ解析研究が非常に楽しいと思っています。データ解析で望むのは触媒の例でいえば手元にない、高性能触媒の設計というケースが多いと思います。しかし、手元にないデータの予測は外挿にあたることが多く、データ科学的手法を用いた高性能触媒の予測はかなり難しいという印象を持っています。反応の解釈のための回帰分析であれば、たとえ高活性触媒の予測ができなくても、反応機構に関する知見が得られます。その解釈性が高ければ、直感と組み合わせて、高性能触媒の設計が可能になることさえあります。分析手法としての解釈のためのデータ解析は、NMRや単結晶X線構造解析などといった分析手法に匹敵するポテンシャルを持っているものと期待しています。

次回以降、解釈のためのデータ解析手法であり、有機反応の回帰分析・データ科学の原点のひとつとも言えるHammett則に関してもう少しだけ詳細に見ていきたいと思います。ここでHammett則では線形回帰を用います。回帰という言葉をここまで当たり前のように出してきましたが、次回は線形回帰のより詳細な背景知識について説明していきます。その後に、Hammett則/線形回帰で有機反応に関するどのような情報を得ることができるのかを見ていきます。