前回はSigmanらの不斉触媒反応の重回帰分析をRで行いました。今回の記事では線形重回帰の背景にふれます。まずはこの記事で述べた単回帰における最小二乗法を示します。下図のように実験値\( y_i \)と予測値\( \hat{y}_i =\beta_0 + \beta_1x_i \)間の誤差の二乗和\( \displaystyle \sum_{i=1}^n \varepsilon_i^2 = \sum_{i=1}^n \{ y_i – (\beta_0 + \beta_1x_i) \}^2 \)を最小化するようにβを決定し回帰モデルを生成します。
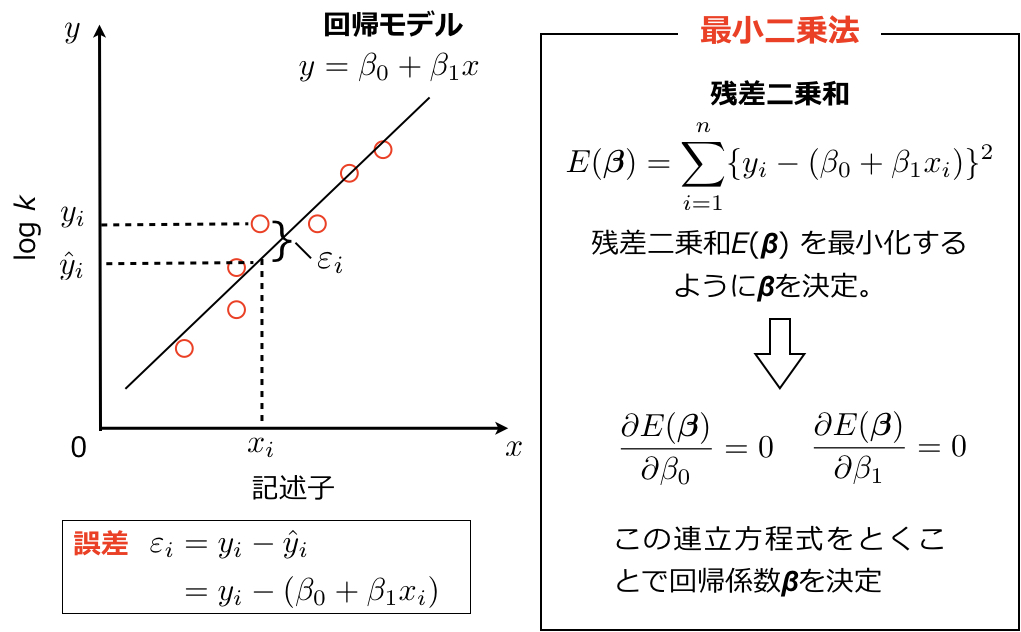
これを複数の記述子を使った重回帰の形式にしてみます。下図に示すように、単回帰のときと同様、実験値yと予測値Xβの間の誤差二乗和(下図の目的関数)を最小化するようにβに関して偏微分して変形すると回帰係数\( \hat \beta \)が求まります。

回帰係数\( \hat \beta \)には記述子行列\( {\bf{X}} \)からなる逆行列\( ({\bf{X}}^\mathsf{T}{\bf{X}})^{-1} \)が含まれています。筆者の分子場解析の説明の際により詳しく述べますが、相関の強い記述子をつかっていたり、サンプル数より記述子の数が多かったりすると、逆行列\( ({\bf{X}}^\mathsf{T}{\bf{X}})^{-1} \)が求めにくい、あるいは存在しなくなります。逆行列\( ({\bf{X}}^\mathsf{T}{\bf{X}})^{-1} \)を直接求めるのではなく、たとえば\( {\bf{X}} \)のQR分解を用いて回帰係数を求めるといった方法があり(統計的学習の基礎を参照)、前回の記事で見たようにRなどプログラミング言語に用意されている関数を用いれば簡単に回帰係数を求めることができます。
決定した回帰係数から解析対象に関するなんらかの情報を得ることもできます。この記事でHammett則では回帰係数(反応定数ρ)の正負および絶対値の大小で反応機構に関する情報が得られることを述べました。重回帰においてもその回帰係数から反応機構に関する情報を抽出したい場合があります。ここで重回帰では複数の記述子を使うため、その単位等が異なることがあります。尺度が大きく異なる記述子間にかかる係数を比較する場合は各記述子の平均が0、標準偏差が1となるように下図のように記述子の標準化を行います。
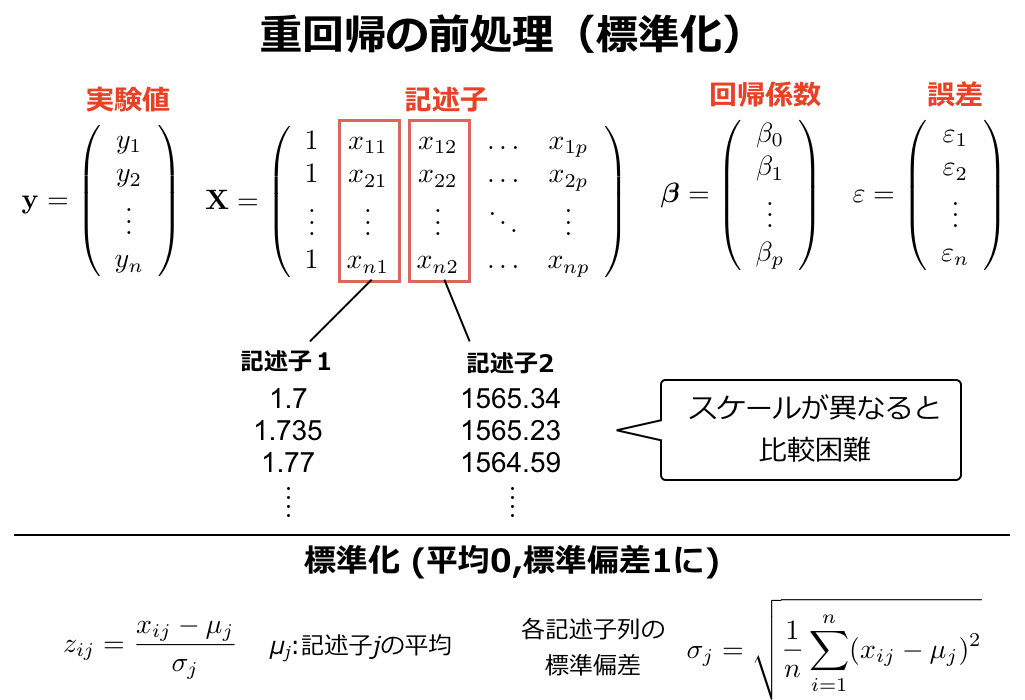
実際に標準化した記述子を用いて解析を行ってみます。前回の記事のSigmanらのデータの線形回帰のスクリプトにxの標準化をいれてみます。
#データの読み込み
y_training <- read.table("data/NHK_training.txt",row.names = 1)
y_test <- read.table("data/NHK_test.txt",row.names = 1)
x_training <- read.table("data/NHK_descriptor.txt",row.names = 1, header = TRUE)
x_training <- scale(x_training) #記述子の標準化
x_test <- read.table("data/NHK_test_descriptor.txt",row.names = 1, header = TRUE)
#回帰分析
fit <- lm(as.matrix(y_training) ~., data = as.data.frame(x_training))
result <- step(fit, direction = "both")
summary(result)これを実行すると結果は以下となります。回帰係数の値が前回と変わっています。
Call:
lm(formula = as.matrix(y_training) ~ B1L + B5L + B1S + LS + B1LB1S +
LLB5S + LLLS, data = as.data.frame(x_training))
Residuals:
Min 1Q Median 3Q Max
-0.39065 -0.07538 0.00024 0.10075 0.29739
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.09480 0.03080 35.547 < 2e-16 ***
B1L 0.59839 0.16398 3.649 0.00141 **
B5L -0.05884 0.04182 -1.407 0.17343
B1S 0.31175 0.12401 2.514 0.01976 *
LS -0.17631 0.07298 -2.416 0.02445 *
B1LB1S -0.31573 0.19268 -1.639 0.11551
LLB5S -0.22052 0.09402 -2.345 0.02843 *
LLLS 0.26130 0.11892 2.197 0.03882 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.1687 on 22 degrees of freedom
Multiple R-squared: 0.8989, Adjusted R-squared: 0.866
F-statistic: 27.93 on 7 and 22 DF, p-value: 1.546e-09
さてここから重回帰のポイントのひとつである変数選択について見ていきます。前回の記事でも述べた通り、記述子が多い場合には訓練データに過剰にフィッティングし外部データに対する予測能が落ちる過学習が起こります。このため単回帰と異なり、重回帰分析の場合はモデル作成の際に少しややこしい手続きが必要になります。まずは過学習についてパターン認識と機械学習の一章を参考に見ていきます。
下図はsin(2πx)(緑の曲線)の関数をもとにガウス分布に従う誤差を足すことで複数の観測点(青い点)を出したものです。この青点を訓練データとして線形重回帰分析を行い、真の関数であるsin(2πx)を推定する問題を考えます。回帰分析には多項式基底を用います(\( y = \displaystyle \sum_{j=0}^p \beta_j \phi_j ({\bf{x}}) \)のようにxの関数の線型結合で表される回帰モデルを線形モデルとよび、またxの関数 \( \phi_j ({\bf{x}}) \)のことを基底関数といいます [パターン認識と機械学習参照] )。3次までの多項式基底を用いた場合には作成した回帰モデル(赤線)は真の関数(緑線)に近いものとなっています。一方で、9次までの多項式基底を用いた場合、回帰モデル(赤線)は訓練データに過剰にフィットしており、もし外部データを当てはめて予測を行なった場合、真の値(緑線上)からは大きく外れたものとなります。
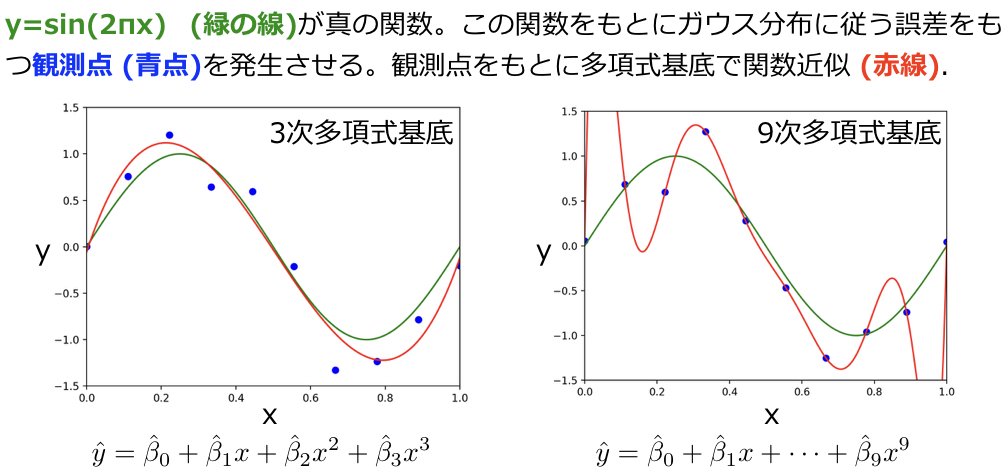
過学習を防ぐために、重回帰分析ではどの変数を用いるか取捨選択(変数選択)を行う必要があります(上記の場合では3次の項までを用いるなど)。変数選択のためのさまざまな評価基準が知られています。そのうちのひとつに以下のAIC(赤池情報基準:Akaike Information Criterion)があります。
AIC = –2ln(尤度) + 2k
AICを用いた変数選択では、AICが最小になるモデルを採用します。前回の記事や上記で用いたRのstep関数は記述子を抜いたりいれたりしながら都度、回帰モデルを構築、AICが最小になるモデルを探索しています。なぜAICが最小となるモデルがよいのかについての説明は以下となります。
この記事で説明した通り、最尤推定の枠組みでみると線形回帰では対数尤度関数(上式の第1項)を最大化するように係数βを決めています。モデルの複雑さがあがり、訓練データに対するフィッティングがよくなるほど対数尤度関数は大きくなります。AICでは対数尤度関数の前にマイナスがついているので、フィッティングがよくなるほど第1項は小さくなります。一方で第2項のkは自由なパラメータ数で、記述子の数が増えモデルの複雑さが増すほど、つまりフィッティングがよくなるほど第2項は大きくなる傾向にあります。第1項と第2項がちょうどよいバランスをとるとき、つまり訓練データに対するフィッティングとモデルの複雑さがちょうどよいバランスをとるときにAICは最小となります。
他によく使うモデル評価基準として交差検証(クロスバリデーション)があります。訓練データをk個のグループに分割し、そのうち一グループを残して回帰モデルを作成、残しておいたサンプルを使ってモデルを評価、このプロセスをk回繰り返します(k-fold cross-validation)。kがサンプル数のとき、とくに一つ抜き交差検証(LOOCV : leave-one-out cross-validation)といいます。
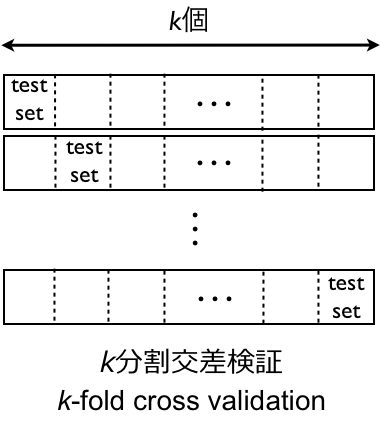
ここでは一つ抜き交差検証で上記のSigmanらのモデルを評価してみたいと思います。モデルから一つずつ訓練データを抜き回帰モデルを作成、抜いたデータを回帰モデルにあてはめ予測値を算出します。この作業をサンプル数分繰り返し、得られた予測値を用いて決定係数を算出します。実際にRでやってみます。上記のRのスクリプトに続けて、以下のスクリプトを実行します。
#選択された記述子のみの行列をつくる
columnList <- c("B1L","B5L","B1S","LS","B1LB1S","LLB5S","LLLS")
x_training_cv <- data.frame(matrix(nrow=nrow(x_training)))
for (i in 1:length(columnList)){
x_training_cv <- cbind(x_training_cv, x_training[, columnList[i]])
}
x_training_cv <- x_training_cv[, -1]
colnames(x_training_cv) <- columnList
x_training_cv
vyploo = c()
#LOOCVの際の予測値を算出
for (i in 1:30) {
cv_fit <- lm(as.matrix(y_training[-i,]) ~., data=x_training_cv[-i,])
yploo <- predict(cv_fit,x_training_cv[i,])
vyploo[i] <- yploo
}
#予測値と実測値をプロット
par(lwd=2,ps=24,pch=16)
plot(as.matrix(y_training), as.matrix(y_predict), col=1, pch=16, asp=1, cex=2, xlab="", ylab="", xlim = c(0.0,2.2), ylim = c(0.0,2.2))
abline(0,1,col="blue")
par(new = T)
plot(as.matrix(y_training), as.matrix(vyploo), col="red", pch=0, asp=1, cex=2, xlab="", ylab="", xlim = c(0.0,2.2), ylim = c(0.0,2.2))
#決定係数の計算
q2 <- 1-sum((vyploo-y_training)**2)/sum((y_training- mean(as.matrix(y_training)))**2)
q2すると下図のような結果が得られ、LOOCVの決定係数q2は0.79となります。
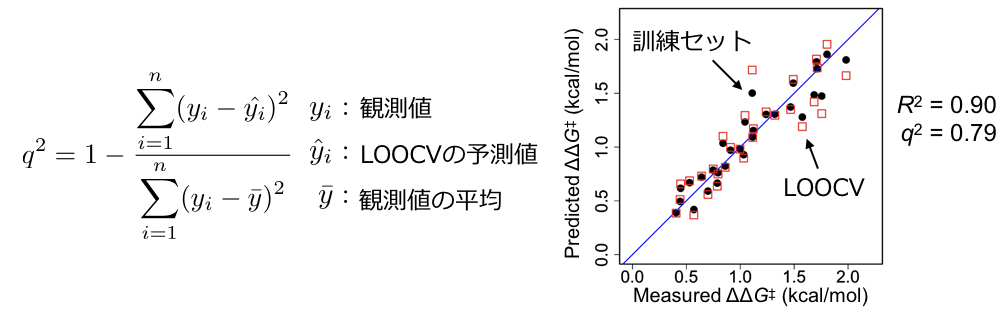
QSARモデル(生物活性を目的変数とした回帰モデル)ではq2 > 0.5が良いモデルとされることがあるようです。このモデル評価、QSAR分野でしばしば議論の対象になります。 QSAR分野でよく使われる回帰モデルの評価基準として以下のGolbraikh-Tropsha criteriaが知られています(Be ware of q2! A. Golbraikh, A. Tropsha J. Mol. Graph. Model. 2002, 20, 269.)。
1. テストセットの決定係数 R2test > 0.6 2. LOOCVで得られる決定係数 q2 > 0.5 3. 原点を含めたテストセットの決定係数R02testあるいはR’02testの値が R2testの値に近い: (R2test −R02test)/R2test or (R2test −R’02test)/R2test < 0.1 かつ 0.85 < k or k′ < 1.15 (k, k′ は 原点を通る、予測値と実測値間の回帰直線の傾き。またk', R’02testは予測値と実測値の軸を入れ替えて計算したk, R02test)
Golbraikh-Tropsha criteriaのポイントとしてはq2 > 0.5(条件2)に加え、テストセットでモデルを評価しその決定係数R2が0.6を超えていること(条件1)、予測値と実測値間の回帰直線のうち原点を含めるものと含めないものが類似していること(条件3)が評価基準として追加されています。条件3はテストセットの予測値と実測値が大きく外れていないことを確認するためのものです(外れていても決定係数が高いことがある)。筆者の経験上、実際の論文では上記に準ずる基準を満たすことに加え、k-foldのクロスバリデーションにより得られた決定係数を示すように求められることがほとんどです。
この他にもさまざまなモデル評価基準があります。一方で、モデルの質にこだわることにどれほどの意味があるのか筆者には判断がつきません。ある程度の閾値を超えていれば、あとは科学的な知見が得られているか、反応条件最適化や分子設計ができているかでモデルの妥当性を判断すればよいのではと思います。データサイエンスの細かい部分を軽視するわけではありませんが、有機合成化学者にとってツールである機械学習部分に労力をかけすぎるのは時間がもったいないと思います。各分野毎にモデル評価などの基準が整えられ、少なくともデータ解析の詳細は論文のSupporting Informationにまわるようになり、データサイエンスにより見出された新しい分子や現象にのみ焦点が当たるようになるのを筆者は楽しみにしています。(どのようなモデルがよいかに関して、ACSのケモインフォマティクスのJounralであるJ. Chem. Inf. Model.にはQSARモデル作成のための指針が示されており、このあたりも参考になるかもしれません。)
前回はどんな記述子を用い、どのような反応・現象を解析すれば新しいデータ解析になるのかについて述べ、また今回は重回帰分析の基礎知識についてふれました。次回は記述子の算出に焦点を当てます。置換基の幅と長さからなる3次元の立体記述子であるSterimol値を計算するPythonのプログラムを見ていきながら、我々有機合成化学者は記述子をどのように計算すればよいのか、そのスタンスについて個人的な意見を書きたいと思います。

コメント