前回までの記事では有機化学の回帰分析・データ科学の基礎であるHammett則についてみていくなかで、有機反応のデータ科学には長い歴史と積み重ねがあることを述べました。またこれまでに積み重ねられてきた有機反応のデータ科学の枠組みを用いて、有機化学的に新しい現象を解析すれば、最先端のデータ科学研究になり得ることを述べました。今回は、その一例としてSigmanらの不斉触媒反応の回帰分析を見ていきます。またSigmanらのデータセットを実際にRを使って解析していきます。
Sigmanらが解析対象とした不斉触媒反応は生成物の立体を制御し、エナンチオマーをつくりわけるための反応です。分子の立体はその生物活性に大きな影響を及ぼすため、不斉触媒反応は医農薬品等ファインケミカル合成に不可欠であり、現代有機合成において必須の反応です。エナンチオマーつくりわけには不斉触媒の形状、大きさ(すなわち立体効果)が重要になります。しかし不斉触媒反応の開発が現在でも研究者の経験知に基づく試行錯誤に依存していることからもわかるように、不斉触媒の最適形状を予測することは至難の業です。不斉触媒の立体構造がどのようにエナンチオ選択性に影響するかを定量化したいと考えるのはごく当然のことかもしれません。その定量化のためにSigmanらはHammett則/物理有機化学の文脈で見出された立体記述子を不斉触媒反応の回帰分析に適用しました。その詳細について述べるにあたり、まずは物理有機化学における立体記述子を見ていきます。
古典的立体記述子(Taft ES)
前回までにみてきた置換安息香酸から計算される記述子であるHammett σは、芳香環上の置換基の電子的効果をあらわす記述子です。立体効果は考慮されていません。1950年代、Taftは立体効果のある系から電子的効果のみを記述するために以下のσ*を考案しました(JACS 1952, 74, 3120. JACS 1953, 75. 4538.)。
σ* = 1/2.48[log (kX/kH)B - log (kX/kH)A]
ここでlog (kX)B、log (kX)Aはそれぞれ塩基性、酸性条件化の脂肪族エステルXCH2COORの加水分解反応速度定数です。σ*の背景にある仮定をHanschらの物理有機化学・QSARのテキストExploring QSARから引用します。
"Hammett式の初期の研究によると、安息香酸エステル類の酸性加水分解におけるρはほぼゼロであり、置換基は電子効果を示さない。一方、塩基性加水分解におけるρは約2である。Taftは、酸性加水分解でのXの効果は純粋に立体的であるが、塩基性加水分解でのそれは、立体効果と電子効果が組み合わさっていると仮定した。したがって上式の第2項は立体パラメータの定義式としても使える"
以下が上式の第2項にあたり、重要な立体記述子であるTaft ESです。
ES = log (kX/kH)A
さらにChartonはCH3やtBuなど対称コマ型置換基のvan der Waals半径がTaft ESと相関があることを見出し、Charton値νを次のように定義しました(JACS 1975, 97, 1552.)。
ν = rX – rH = rX – 1.20 (rXは置換基Xの最小van der Waals半径)
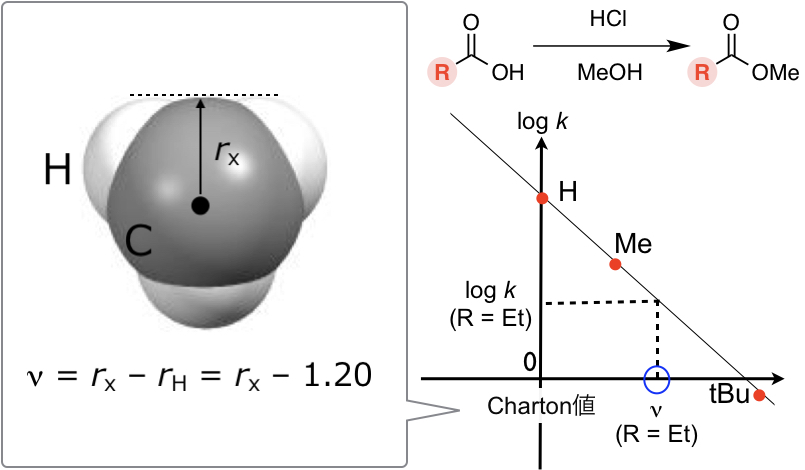
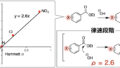
対称コマ型置換基のTaft ESとCharton値νに相関があるとは以下を意味します。すなわち酸性条件化での対応する置換基を持つ脂肪族エステルRCOOMeの加水分解反応(あるいはその逆反応)速度定数の対数(Taft ESと同義)と、Charton値νとをプロットすると上図右のように直線にのります。Et基などの非対称置換基に関しては、その置換基を持つエステルの加水分解(あるいはその逆反応)の反応速度定数の対数を図の回帰式に代入することでCharton値νへと変換します。つまりCharton値νは反応速度定数の対数であるTaft ESを、脂肪族エステルの加水分解反応における“置換基の有効van der Waals半径”のスケールに変換したものとみなせるかと思います。
不斉触媒反応における自由エネルギー関係(回帰分析)
SigmanはこのTaft-Charton値νを用いて不斉NHK(Nozaki-Hiyama-Kishi)反応の単回帰分析を行いました。下図のように、触媒の置換基Rの部分を変えた際の生成物のエナンチマー比の対数を目的変数とし、Taft-Charton値νを記述子として単回帰分析を行い、反応の定量化ができることを見出しています。鏡像異性体比の対数は下図左のように各エナンチオマーへ通じる遷移状態のエネルギー差(ΔΔG‡)に対応します(Curtin-Hammettの原理)。したがって本解析も線形自由エネルギー関係となります。

ここで上の自由エネルギー関係(回帰モデル)の図を見るとTaft-Charton値νが大きくなればなるほど生成物のエナンチオ選択性が向上するのではという期待がうまれます。しかしTaft-Charton値νが大きい置換基をもつ触媒を使って反応を行なってもエナンチオ選択性の向上はできず、下図左のグラフにしめすようにある点から異なる直線にのることをSigmanらは見出しています。
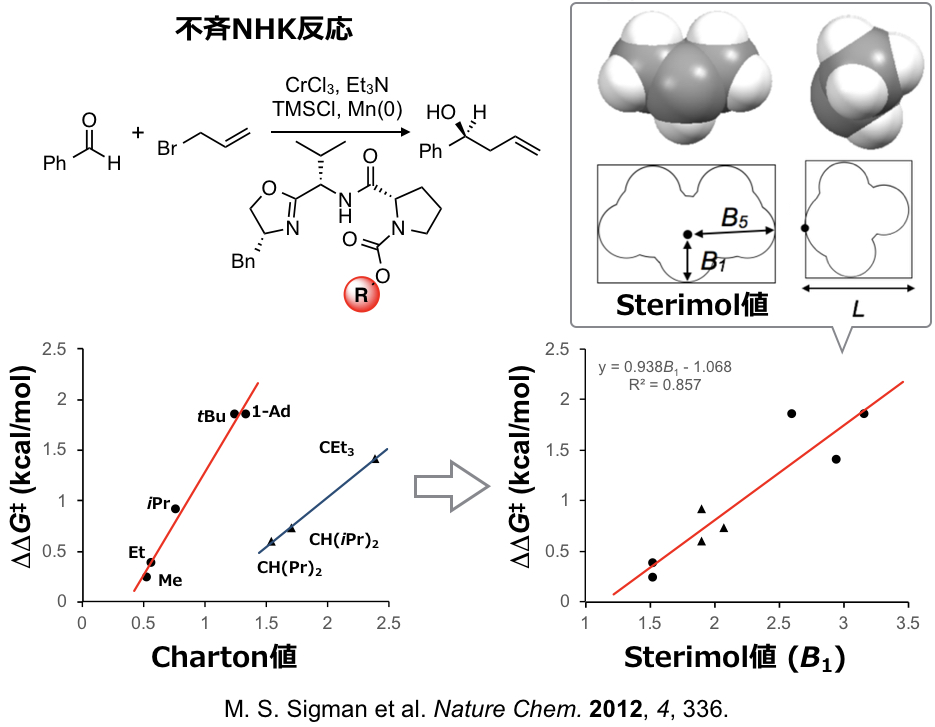
そもそもTaft-Charton値は実験的に求められた脂肪族エステルの加水分解(およびその逆反応)における置換基の“有効van der Waals半径“とみなせるものです。脂肪族エステルの加水分解以外の反応に対して記述能力が高くなくても不思議ではありません。また実験により得られる記述子では適用範囲も限られます。計算機上で算出できる記述子がのぞまれますが、そのような立体記述子として置換基の幅(B1,B5)と長さ(L)からなる上図のSterimol値という3次元の記述子があります。
Sigmanらは上図右のグラフに示すように不斉NHK反応においてTaft-Charton値にくらべSterimol値の方がより記述能が高いことを見出しています。ここでは3次元の記述子をそのまますべて使うわけではなく、置換基の最小の幅B1のみを用いています。つまり置換基のどの部分が選択性に有効かある程度の情報を抽出できます。さらにSigmanらはNHK反応において下図のように触媒および基質のRLおよびRSの部分をかえて反応をスクリーニングし集めたデータおよびSterimol値を記述子として用い、生成物のエナンチオ選択性を重回帰で定量化することに成功しています。
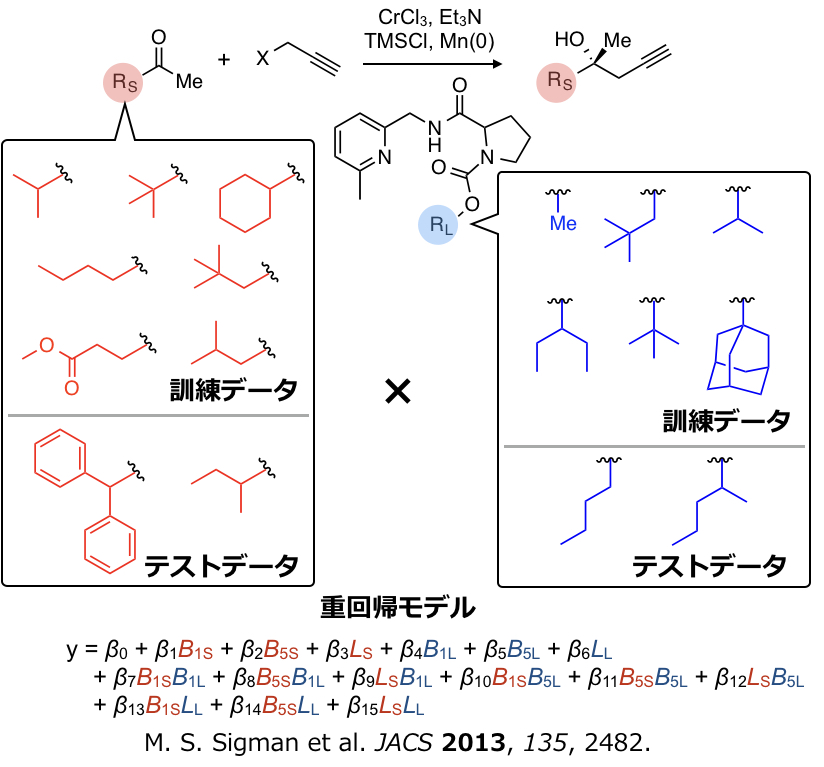
不斉触媒反応のRによる解析
以前その背景を述べた記述子をひとつだけ使う単回帰に加え、複数の記述子を使う重回帰分析をマスターすればこの分野で論文を書くのに役立ちます。重回帰分析の詳細な背景については次回述べるとして、まずは実際に上記のSigmanの解析を例にRで重回帰分析をやってみます。データセットをGitHubに置いてあります。目的変数は生成物のエナンチオマー比の対数(ΔΔG‡)であり、訓練データ、テストデータはそれぞれ30および28サンプル、記述子は15次元となります(基質と触媒の記述子間の交差項が含まれています)。
詳細は次回ご説明しますが、この記述子をすべて回帰モデルに使うと訓練に使ったデータに過剰にフィッティングしてしまい、外部のデータに対する予測能が落ちてしまいます(過学習)。過学習を防ぐために記述子を抜いたり足したりして回帰モデルを作成しその性能を評価、訓練データに対するフィッティングと外部データに対する予測能のちょうどよいバランスを探していきます(ステップワイズ回帰)。ここではAIC(Akaike Information Criterion)をモデル評価基準として用いAICが最も小さくなるモデルを採用することとします(詳細は次回)。
実際にやってみます。解析にはRおよびRStudioを用います。RStudioを開き、 File -> New project -> New directory ->デスクトップなど適当なdirectoryに名前をつけてフォルダを作成(下図ではMFA_catalysisとしています)->生成したフォルダにGitHubからダウンロードした6th内にあるdataフォルダを入れます。左上のプラスマークをクリックしR scriptを選択、ex.Rとして保存します(下図のような状態になります)。

ex.Rに下記の線形回帰のスクリプトを書き込み実行してみます。コマンドの実行には⌘+Enterあるいはctrl+Enter、あるいはRStudio上のRunをクリックします。
#データの読み込み
y_training <- read.table("data/NHK_training.txt",row.names = 1)
y_test <- read.table("data/NHK_test.txt",row.names = 1)
x_training <- read.table("data/NHK_descriptor.txt",row.names = 1, header = TRUE)
x_test <- read.table("data/NHK_test_descriptor.txt",row.names = 1, header = TRUE)
#回帰分析
fit <- lm(as.matrix(y_training) ~., data = as.data.frame(x_training))
result <- step(fit, direction = "both")
summary(result)出力は以下のようになると思います。15個の記述子のなかから7個の記述子が選ばれていることがわかります。
Call:
lm(formula = as.matrix(y_training) ~ B1L + B5L + B1S + LS + B1LB1S +
LLB5S + LLLS, data = as.data.frame(x_training))
Residuals:
Min 1Q Median 3Q Max
-0.39065 -0.07538 0.00024 0.10075 0.29739
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.46806 0.83610 -0.560 0.58126
B1L 0.90491 0.24798 3.649 0.00141 **
B5L -0.06768 0.04811 -1.407 0.17343
B1S 0.69315 0.27573 2.514 0.01976 *
LS -0.17917 0.07417 -2.416 0.02445 *
B1LB1S -0.17709 0.10807 -1.639 0.11551
LLB5S -0.04379 0.01867 -2.345 0.02843 *
LLLS 0.03465 0.01577 2.197 0.03882 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.1687 on 22 degrees of freedom
Multiple R-squared: 0.8989, Adjusted R-squared: 0.866
Estimateのところの回帰係数から、下記のような回帰モデルができていることがわかります(実際の論文ではRではなくMATLABを使っているためかモデルが異なります)。
y = -0.478 + 0.905B1L – 0.068B5L + 0.693B1S – 0.179LS – 0.177B1L•B1S – 0.044 LL•B5S + 0.035 LL•LS
モデルの予測能を評価してみます。詳細は次回ご説明するとして、訓練データおよびテストセットの予測値を実測値に対してプロットし、その決定係数R2およびR2testを計算してみます。
y_predict <- predict(result)
y_test_predict <- predict(result,newdata=x_test)
par(lwd=2,ps=24,pch=16)
plot(as.matrix(y_training),as.matrix(y_predict)
,col=1, pch=16, asp=1, cex=2, xlab="", ylab="", xlim = c(0.0,2.2), ylim = c(0.0,2.2))
abline(0,1,col="blue")
par(new = T)
plot(as.matrix(y_test),as.matrix(y_test_predict)
,col="red", pch=0, asp=1, cex=2, xlab="", ylab="", xlim = c(0.0,2.2), ylim = c(0.0,2.2)) これを実行すると下図のようになると思います。青色の直線はy = xです。予測値と実測値をプロットすると理想的にはすべてこの直線上に乗ります。訓練データ(黒点)、テストデータ(赤い四角)ともにわりときれいに直線上にのっていることがわかります。
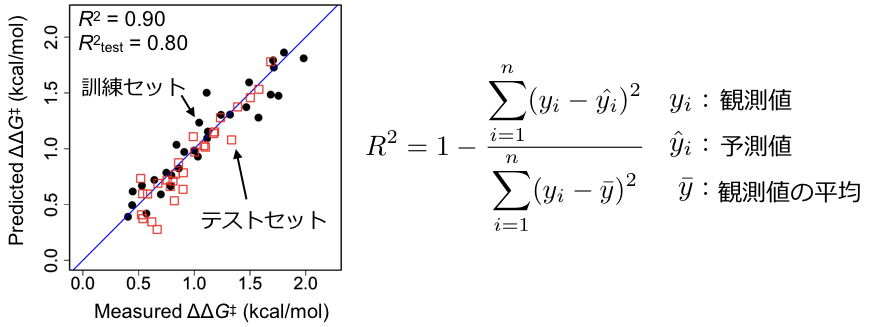
モデル評価基準の一つである上図右に示した決定係数を計算します。以下を実行すると訓練データおよびテストデータの決定係数はそれぞれR2=0.90, R2test=0.80となります。
R2_training <- 1-sum((y_predict-y_training)**2)/sum((y_training-mean(as.matrix(y_training)))**2)
R2_training
R2_test <- 1-sum((y_test_predict-y_test)**2)/sum((y_test-mean(as.matrix(y_test)))**2)
R2_testQSAR分野での良い回帰モデルの条件のひとつであるR2test>0.60を満たしています(A. Golbraikh, A. Tropsha, J. Mol. Graph. Model. 2002, 20, 269.)。解析は以上になります。このようにデータさえ集めれば回帰分析(機械学習)自体はわりとすぐにできます。以前にも述べたように機械学習は前処理までが8割ですので、有機合成化学者は機械学習の部分ではなく、どのような反応をどのような記述子を使って解析するかに注力することで、Sigmanらのように重要な研究を展開できます。
まとめ
今回の記事では記述子としてCharton値およびSterimol値の例をご紹介しましたが、Sigmanらはさらに記述子を探索し、不斉触媒反応の線形重回帰分析のための枠組みを構築しています(M. S. Sigman et al. Acc. Chem. Res. 2016, 49, 1292. Chem. Sci. 2018, 9, 2398.)。回帰係数などをもとにさまざまな反応でメカニズムの解釈や分子設計を行なっています(線形重回帰に基づくメカニズムの解釈や分子設計の例は筆者の分子場解析をもとに説明します。)。
このように不斉触媒反応というHammettの時代には一般的でなかった有機化学の新しい現象を古典的物理有機化学の枠組みで解析し、その改善を行うことで自然と新しい研究となります。この分野は触媒インフォマティクスの一分野ともみなせるかと思います。ここまでご説明してきたように、分子性触媒のインフォマティクスは“触媒化学”+”ケモインフォマティクス”という足し算で構成される分野ではなく、物理有機化学から続く有機化学の一分野であると筆者は考えています。自然科学の分野にはその分野に特化したデータサイエンスがあり、それを発掘できる可能性が高いのはその分野に向き合ってきた専門家なのではと思います。たとえばSigmanらが用いたCharton値やSterimol値はともに物理有機化学・QSARのテキスト” Exploring QSAR”に紹介されているものです。物理有機化学やQSARの文脈で開発されてきた記述子の中には、まだまだ現代有機化学のデータ解析に適した記述子が隠されているかもしれません。
次回以降は今回簡単に触れるのみであった線形重回帰についてより詳しく見ていきます。またPythonによりSterimol値を計算するプログラムを書いてみたいと思います。その後に筆者の見出した分子場解析の枠組みを見ていきます。

コメント