Hammett則と最尤推定 - 分子場解析入門

前回は有機反応の少数サンプルの回帰分析の源流とも言えるHammett則についてふれました。今回はHammett則を例に、線形回帰について少し詳しくみていきます。

Hammett則では記述子(\(x\))としてσを、目的変数(\(y\))としてエステルの加水分解の反応速度定数の対数を用いて回帰モデル\( y=\beta_0+\beta_1 x \) を作成します。ここで\(x\) と\(y\) の呼び方を下図にまとめました。\(y\)の呼び方は定まっていない印象ですが、化学分野では\(x\) は記述子(descriptor)と呼ばれることが圧倒的に多いです。

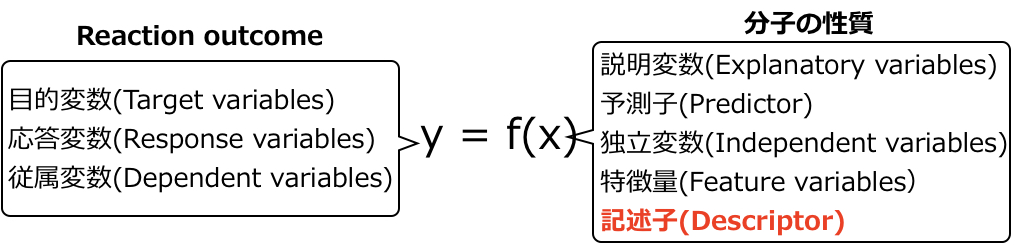
今回は化学の話ではなく、線形回帰に焦点をあてます。まずはHammett σを記述子として使った回帰分析を実際にやってみます。前回の記事の通り、Hammett σは置換安息香酸の酸解離定数から計算される記述子です（下図）。

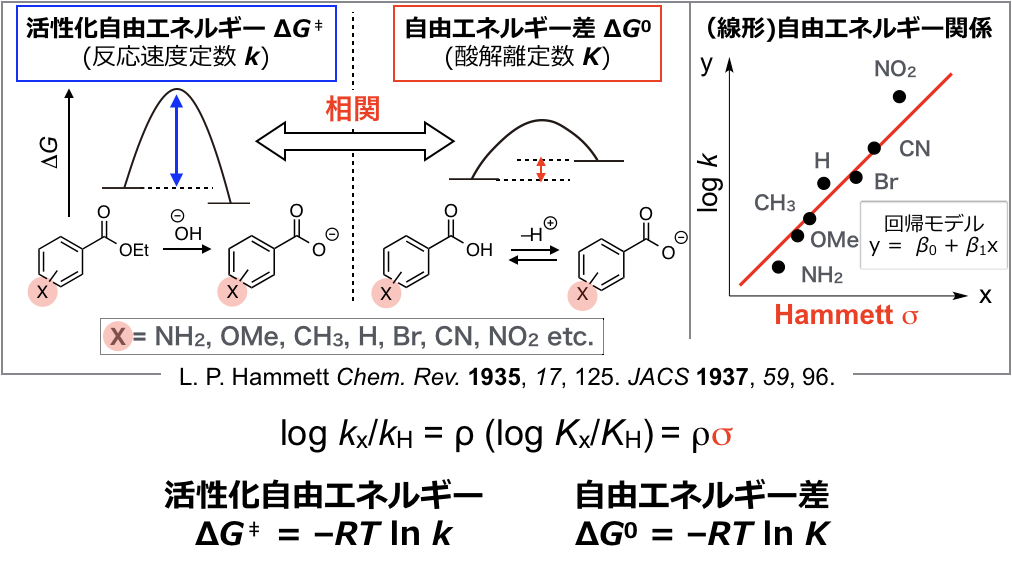
下記にHammett σの実際の値を示します（簡単のためにパラ位に置換基をもつ安息香酸から計算したもののみ）。この記述子を用いて、上図にそのイメージを示すように、置換安息香酸エステルの加水分解速度定数の対数（log k）を目的変数として、回帰モデルを作成します。目的変数の値をテーブルの最下段に示します。

置換基X	-OMe	-Me	-H	-Cl	-NO₂
Hammett σ	-0.268	-0.170	0	0.062	0.778
log k_X/k_H	-0.667	-0.327	0	0.638	2.019

k_xは置換基Xをもつ安息香酸エステルの加水分解反応速度定数

この値をエクセルにコピペします。「挿入」->「散布図」を選択してプロットすると下図左のようになります。さらにプロットした点付近で右クリック、「近似曲線を追加」し、「グラフに数式を表示する」および「グラフにR2乗値を表示する」を選択してみたものが下図右になります（筆者はMac OSでExcel 2019を使っています。グラフのレイアウトはデフォルトから変更）。前回示したHammett式（log k_x/k_H = ρ(log K_x/K_H) = ρσ）からわかるように切片（回帰モデル\(y=\beta_0+\beta_1x\)のうち\(\beta_0\)）は0なので、エクセル上の近似曲線の書式設定で、切片を0にします。

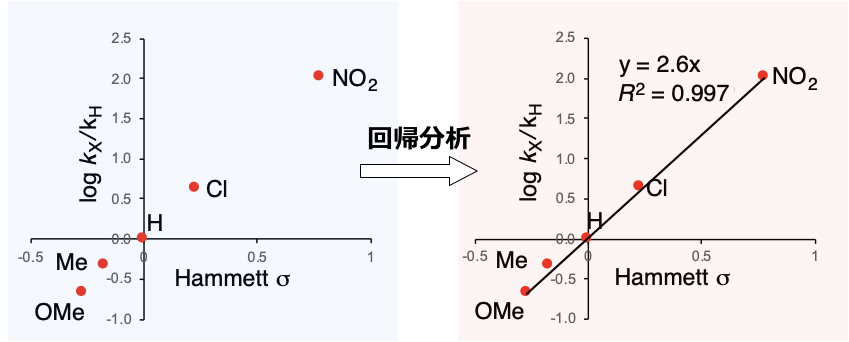
y=2.6x、つまり傾き2.6の回帰式が得られました。R² = 0.997 であり(1に近いほど、あてはまりがよい)、プロットが綺麗に直線上にのっていることがわかります。この回帰モデルにHammett σを代入すれば、置換安息香酸エステルの反応速度が予測できます。最小二乗法/線形回帰も機械学習手法の一種ですので、Hammett式もAI/人工知能とみなせます。上記でHammett式を作成すれば、有機反応予測のための人工知能を作ったことがあると言うことができます。

さて回帰モデルを作成してみました。前回述べたようにハメット則では回帰係数等から反応機構に関する情報が得られます。その詳細は次回述べるとして、今回は回帰係数をどのように決定し回帰モデルを作成するか、つまり最小二乗法について単回帰であるHammett式を例に詳しく見ていきたいと思います（単回帰 [univariate regression]: 上記の例のように記述子がひとつの回帰。記述子が複数のものは重回帰とよぶ）。

下図にそのイメージを示すように、記述子σ(x軸)と反応速度定数の対数(y軸)をプロットします。回帰式 \(y=\beta_0+\beta_1x\) の\(x\)にHammett σの値を代入した際に、予測値と実測値の誤差が最も小さくなるように回帰係数\(\beta_0\), \(\beta_1\)を決めることで回帰モデルを作成します（今回のHammett式では\(\beta_0=0\)ですが、説明上\(\beta_0\)も含めます）。回帰モデルに記述子の値\(x_i\)を代入したときの反応速度定数の予測値を\(\hat y_i\)とし、対応する訓練データの反応速度定数を\(y_i\)とすると予測誤差は\(\varepsilon_i = y_i – \hat y_i \)となります（下図）。

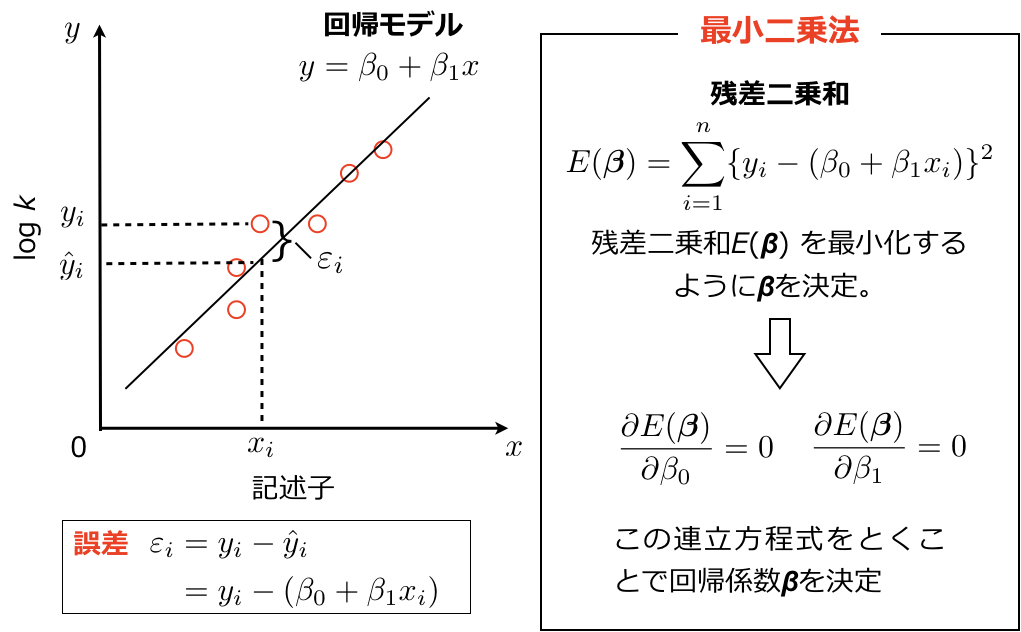
通常はこの予測誤差の2乗和\( \displaystyle \sum_{i=1}^n \varepsilon_i ^2 \)、すなわち上図中に示した残差二乗和（RSS: residual sum of square）を最小化するように係数\(\beta_0\), \(\beta_1\)を決めます。

残差二乗和は下に凸の関数であるので、誤差を最小化するには\(\beta\)について偏微分したものを０とした、上図に示した連立方程式を解くことで回帰係数を決めることができます。

上記の最小二乗法の説明はよく目にしますし、解析的にとける二乗和を用いるのは直感的にも自然のように思います。一方で、この最小二乗法の後ろには確率分布が隠れています。ここでは最小二乗法のより大きな枠組みである最尤推定（Maximum Likelihood）についてご説明したいと思います。

最尤推定

最尤推定とは、最も尤もらしい（もっともらしい）母数（確率分布を特徴づける定数）の値を求める、という意味です。以下の統計学の教科書からエッセンスのみを述べます。

最尤推定の手続きは以下のようになります。既知の確率分布を考えた時にその母数（確率分布を特徴づける定数）を\(\theta\)とします。n個の標本を抽出したとき、データが\(x_i\)をとる確率を\(f(x_i,\theta)\)とすると、観測した標本の状態をとる確率は積をとって以下になります。

尤度関数: \( L(\theta) = f(x_1,\theta) \cdot f(x_1,\theta) \cdot f(x_2,\theta) \cdots f(x_n,\theta)=\displaystyle\prod_{i=1}^n f(x_i,\theta)\)

上記を尤度関数とよび、この尤度関数を最大化するような母数\(\theta\)を求めるのが最尤推定です。\(\theta\)について微分を行ったものが0になるように（関数が極大をとるように）\(\theta\)を決めます。積の形のままだと計算が大変な場合が多いので、対数をとり以下の対数尤度関数としてから計算することが多いです。

対数尤度関数: \( \ln L(\theta) = \ln \displaystyle\prod_{i=1}^n f(x_i,\theta)\ = \sum_{i=1}^n \ln f(x_i,\theta) \)

具体例を考えます。3回コイン投げをして（表、表、裏）というデータが得られた際の、コインを投げたとき表がでる確率\( p \)を推定する問題を考えます。その尤度関数は\( L(p) = p^2\cdot (1-p)\)となります。この場合は対数尤度関数としなくても尤度関数を微分して\( 0 \)（ \( L(p)/ \partial p = 2p–3p^2 = 0\) ）とすることで、2項分布の母数\( p \)を推定できます (\( p = 2/3 \))。

以上が最尤推定です。では最尤推定の枠組みを用いて線形回帰を見ていきます。以下の本の第1章を参考に説明します。

最小二乗法では予測誤差\(\varepsilon_i\)の二乗和を最小化するように回帰係数の値を決め、回帰モデルを生成しました。ここで予測誤差\(\varepsilon_i\)がガウス分布に従うとします(英語版のパターン認識と機械学習は公開されていますので、リンク先のFigure 1.16を見てください)。ガウス分布の母数は下図に示すように平均\(\mu\)と分散\(\sigma^2\)です。

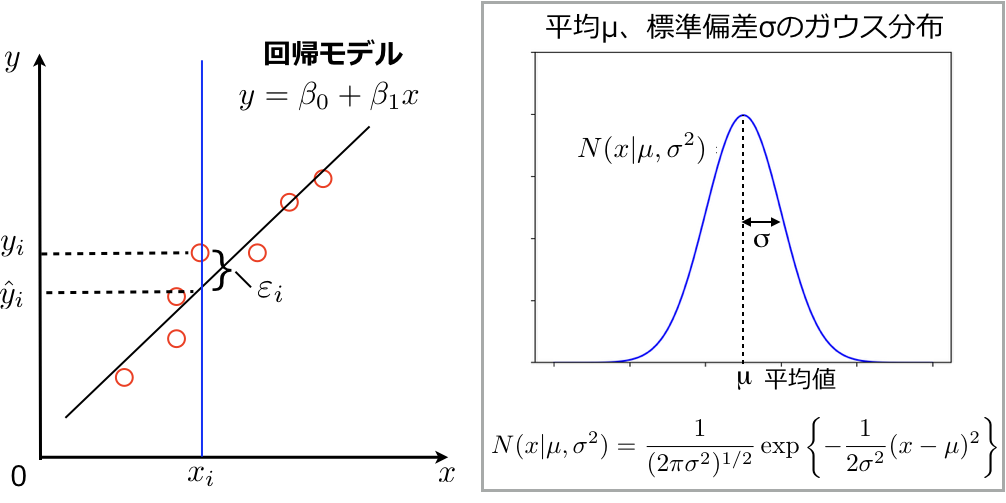
すなわち観測値\( y_i \)は真の値（上図のガウス分布の平均値）に標準偏差\( \sigma \)のガウス分布に従うノイズを加えたものとなります。真の値の推定量が\( \hat y_i \)となるので、観測値\( y_i \)をもとに推定されるガウス分布は\( N(y_i | \hat y_i, \sigma^2)\)となります（イメージがわきにくい場合は、パターン認識と機械学習のFigure 1.16を見てください)。すなわち線形回帰のモデリングは、ガウス分布の母数の最尤推定を行い推定量 \(\hat y = \beta_0+\beta_1x\) を求める問題となります。最尤推定の手続きのところで示した通り、尤度関数を最大化するように母数の推定量 \(\hat y_i = \beta_0+\beta_1x_i\) を求めます。\(y_i\)が従う確率分布は\( N(y_i | \hat y_i, \sigma^2)\)なので尤度関数は以下になります。

尤度関数：\( \displaystyle\prod_{i=1}^n N(y_i | \hat y_i, \sigma^2)\ \)

最尤推定の手続きのところで示したように、このままだと計算が大変なので、対数をとって和の形にします。ガウス分布の式は上図内に示した通りなので、対数尤度関数は以下のようになります。

対数尤度関数：\( \ln \displaystyle\prod_{i=1}^n \frac{1}{(2\pi\sigma^2)^{1/2}} \exp \{-\frac{1}{2\sigma^2} (y_i – \hat y_i )^2 \} = -\frac{1}{2\sigma^2} \displaystyle \sum_{i=1}^n (y_i- \hat y_i )^2 – \frac {n}{2} \ln \sigma^2 – \frac {n}{2} \ln (2\pi) \)

これを最大化するように\(\hat y_i = \beta_0+\beta_1x_i\)を定めればよいわけです。上式で\(\hat y_i\)がでてくるのは、 \( -\frac{1}{2\sigma^2} \displaystyle \sum_{i=1}^n (y_i- \hat y_i )^2 \)の部分のみです。定数の部分を除外し、マイナスがついていることを考えると、\( \displaystyle \sum_{i=1}^n (y_i- \hat y_i )^2 = \displaystyle \sum_{i=1}^n \{y_i- (\beta_0+\beta_1x_i) \}^2 \)の部分を最小化するように係数\( \beta_0\)、\( \beta_1\)を決定すればよいことになります。この式は最初にご説明した残差二乗和（RSS: residual sum of square）となっています。

このように最小二乗法を最尤推定の枠組みで考えると、ガウス分布から残差二乗和がでてきます。有機合成が専門の筆者は機械学習・統計学を勉強した際にこのことを知って大変驚きました。

今回はHammett則の背景のひとつである線形回帰について見ました。ハメット則では回帰係数等から反応機構に関する情報が得られます。次回は、Hammett則により反応に関するどのような情報が得られるかについて見ていきます。