前回までで不斉触媒反応の重回帰分析を論文化するために必要な基礎知識のうち、どのようなスタンスで反応を解析すればよいのか、また詳細なバックグラウンドとして重回帰分析のモデル構築・評価について議論しました。今回は有機合成化学者がオリジナルなデータ解析研究を展開する上で必須となる記述子をどのように計算すればよいのかについて筆者の考えを述べます。
データ解析の主軸とも言える回帰分析では、反応を定量的に表現するために、反応活性と分子の性質を数値化した記述子とを相関付けします(下図)。
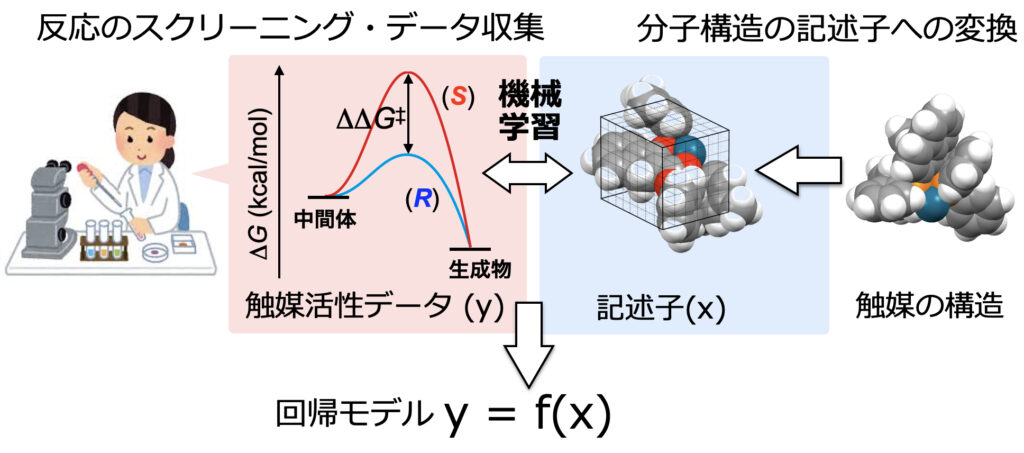
実験をして、日々データと向き合っていれば、分子のどの部分の立体や電子的性質が反応に効いていそうかなどといった、記述子のイメージは自然と持っている場合が多いのではと思います。実験をしているからこそ身につけられる有機合成化学者の記述子に関する高解像度は、データ科学を展開する上できわめて重要であると筆者は考えています。
では自分のイメージとして持っている記述子をどう算出すればよいでしょうか?芳香環上の置換基の電子的性質を定量化したければ、以前の記事で述べたようなHammett σや、それに類する記述子を使えばよいかと思います。
一方で、なかなかイメージにちょうどよくフィットする既存の記述子が見つからない、あるいは使いたい記述子はあるけれども、その記述子を計算するための使いやすいソフトウェアがないという場合もあるかと思います。私自身、本サイトでのちのちご紹介していく分子場解析の記述子を計算する際に、当時お世話になっていた理論化学の研究室の助教の方に、どんなソフトを使えばよいのかわからず困っていると相談したことがあります。
有機合成化学者である筆者としては、その回答が強く印象に残っています。それは以下のようなものであったと記憶しています。
プログラムは書けるものであれば書いてしまえばよい
有機合成分野での指導教員には、しっかり汗をかけ、と教わりました。計算化学分野でも、やはり自分でしっかり汗をかくこと、手を動かすことが重要なのかなと思わされるコメントでした。
というわけで、本記事では、この記事でもご紹介した計算機上で算出できる立体記述子であるSterimol parameter(下図)を題材に、Pythonを使って実際に記述子を自分の手で算出してみたいと思います。ちなみに繰り返しますが、筆者自身は有機合成化学者であり、情報科学の専門的な教育は受けていないことは付記しておきたいと思います。
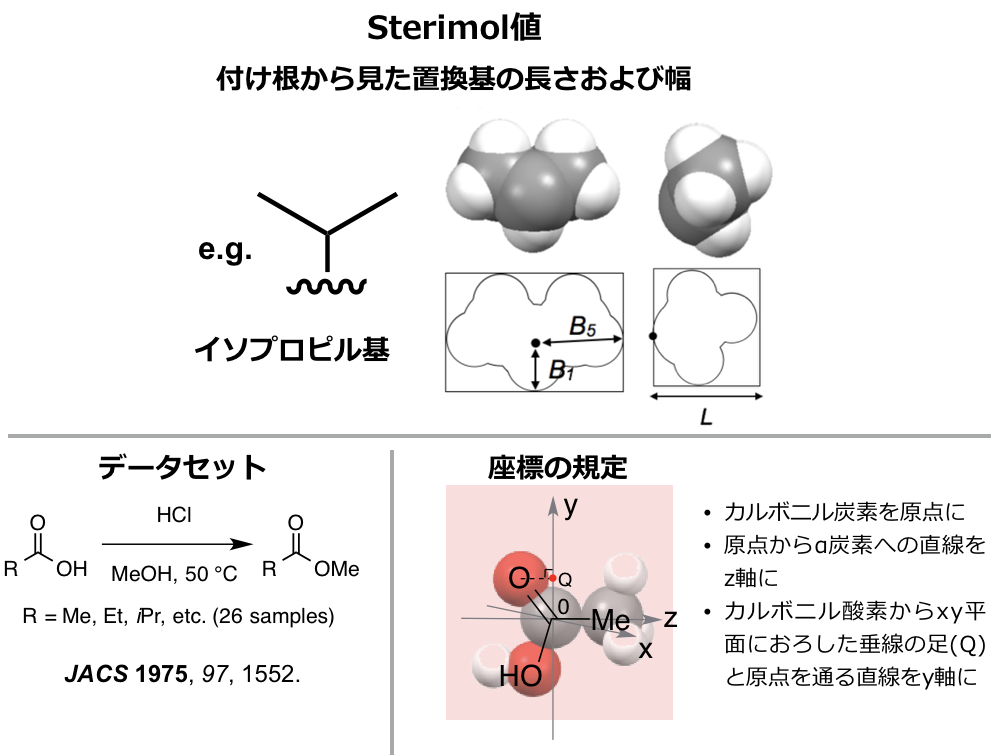
Sterimol parameterを算出する分子構造として、この記事でご紹介した代表的な立体記述子であるTaft-Charton値を算出・検証するのに使用された脂肪族カルボン酸のうち26サンプルを用いてみます(上図左下:JACS 1975, 97, 1552.)。
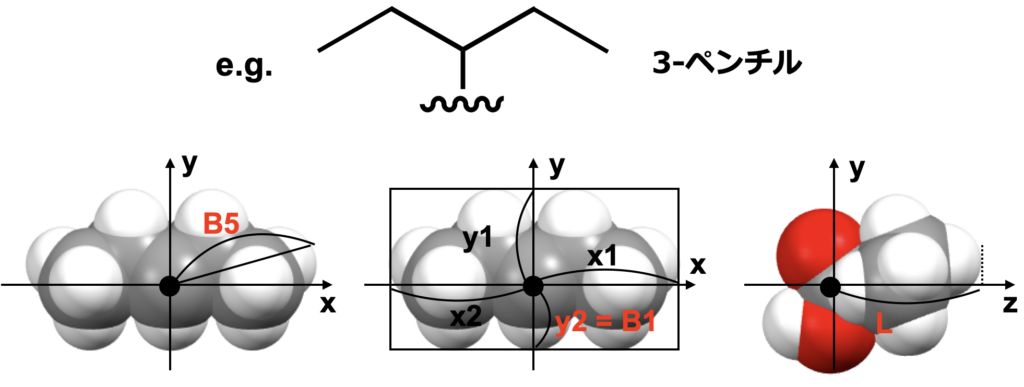
構造はGaussian09を用いてB3LYP/6-31G(d)レベルで最適化したものを用います。Sterimol parameterは上図のような置換基の最大、最小の幅と置換基の長さからなる3次元の記述子です。この幅と長さを求めるために、上図右下のようにカルボニル炭素を原点に、カルボキシ基のα炭素と原点(カルボニル炭素)を通る直線をz軸に、カルボニル酸素からxy平面上におろした垂線の足と原点を通る直線をy軸に設定してみます。このように設定することで、下図のように幅は置換基をxy平面に射影したものから、長さは分子をyz平面に射影したものから求められそうです。
- 最大の幅は、単純にxy平面上に射影した置換基上の原子の原点からの距離を測り、その最大のものになりそうです(B5)。
- 最小の幅は、図のようにx1,x2,y1,y2の長さのうち最も小さいものでどうでしょうか(B1)。
- 少しオリジナルの定義とは異なりそうですが、長さは単純に図のように原点から最も遠い水素原子のz座標から計算できそうです(L)。
今回の計算では、分子構造の配列も重要なポイントですが、のちのちご紹介する分子場解析でも同様の分子の配列をおこなっていくので、配列の具体的なプログラムについてはその際見ていきます。今回は座標をすでに揃えてあるxyzファイルをGitHubに置いてあります。これを使ってSterimol parameterを計算していきます。
今回はエディタとしてAtomを使って解析してみます。Sterimolフォルダをデスクトップにつくり、GitHubからダウンロードしてきたxyzファイルをおきます。そのフォルダをprojectととして開きます。Atomのpackageであるterminal-plusをインストールし、ターミナルからPythonを実行できるようにしておきます(筆者はMac OSを使っています。またAtomの日本語化含む種々のPackageのインストールに関しては他サイトを参照)。
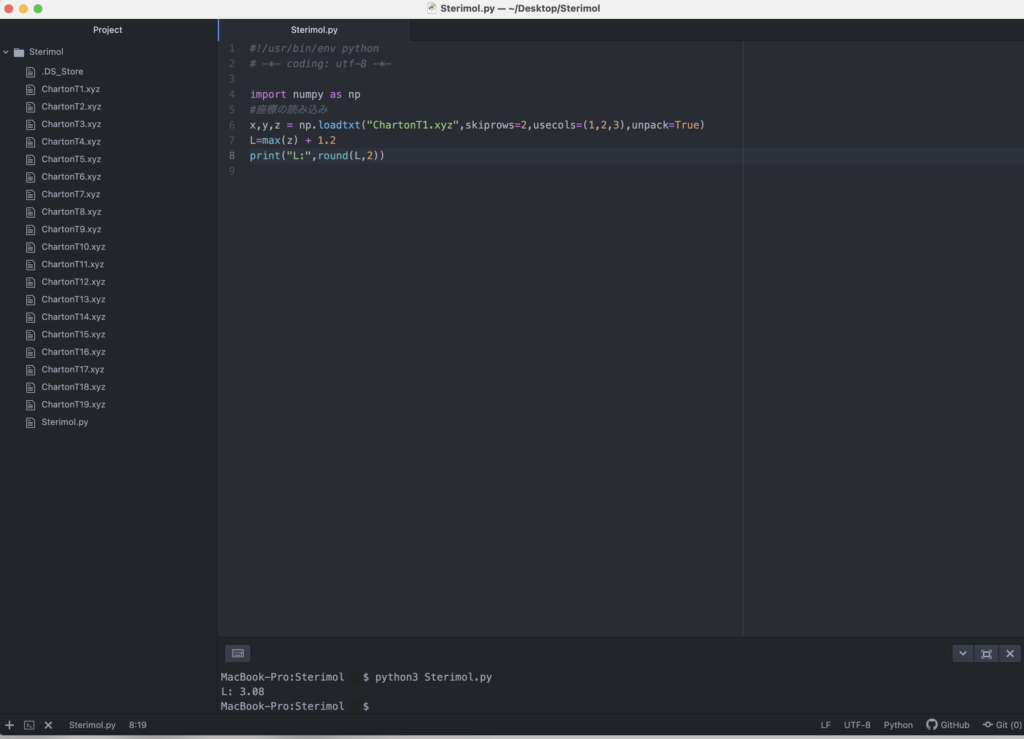
フォルダ内でSterimol.pyというファイルをつくり、この中にPythonのプログラムを書いていきます。まずは酢酸(ChartonT1.xyzに対応)を例にSterimol値を計算してみます。最初はファイルの読み込みです。xyzファイルでは3行目以降は、1列目に原子名、2~4列目に対応する原子のx,y,z座標がそれぞれ記されています。変数x,y,zに対応する座標を代入します。
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy as np
#座標の読み込み
x,y,z = np.loadtxt("ChartonT1.xyz",skiprows=2,usecols=(1,2,3),unpack=True)今回は炭素と水素のみからなる置換基を用いているので最も原点から遠い原子として水素原子のみを考慮していきます。z座標の最大値に水素のファンデルワールス半径1.2 Åを足したものが置換基の最大の長さLです。下記を実行すると3.08という値が得られると思います。
#z座標のなかから最大値を抽出し、水素のファンデルワールス半径1.2 Åを足す。
L = max(z) + 1.2
print("L:",round(L,2))ちなみにAtomの実行画面等は以下のようになります。ターミナル上でPython Sterimol.pyと打ち込んで実行する形です。
次に、最小および最大の幅(B1およびB5)を算出していきます。上述のように最大の幅B5は、単純にxy平面上に射影した置換基上の原子の原点からの距離を測り、その最大のもの、最小の幅B1は、上図に示したようにx1,x2,y1,y2の長さのうち最も小さいものとして計算していきます。今回は炭素と水素のみからなる置換基を用いているので水素原子のみを考慮していきます。
まずは水素原子の数を数えましょう。xyzファイルの中の原子名を読み込み、変数Atomsに代入します。また原子数をnumber_atomsに代入します。
#原子名の読み込み
Atoms = np.loadtxt("ChartonT1.xyz",skiprows=2,usecols=(0,),unpack=True,dtype='S3')
#全原子数
number_atoms = len(x)Atomsに含まれる水素の数を数えます。
#水素の数をnumber_Hに格納
number_H = 0
for i in range(number_atoms):
if Atoms[i] == "H".encode():
number_H = number_H + 1それぞれ、xy平面上に射影した水素の原点からの距離、x座標、y座標を代入するためのゼロベクトルを作ります。ただし、カルボキシ基上の水素は除くため、次元数を1つ減らします。
B5 = np.zeros(number_H-1)
x_B1 = np.zeros(number_H-1)
y_B1 = np.zeros(number_H-1)xy平面上に射影した水素原子の原点からの距離、x座標、y座標をそれぞれ代入します。
#xy平面上に射影した全原子の原点からの距離
distxy = np.sqrt(x**2 + y**2)
j = 0
for i in range(number_atoms):
#カルボキシ基上の水素以外の水素の、xy平面上に射影した水素の原点からの距離、x座標、y座標を代入(今回のxyzファイルでは、カルボキシ基の水素は上から4つ目に統一)
if i != 3 and Atoms[i] == "H".encode():
B5[j] = distxy[i]
x_B1[j] = x[i]
y_B1[j] = y[i]
j = j + 1B5は水素原子の原点からの距離のなかで最大のものなので以下になります。実行すると2.23という値が出力されます。
B5 = max(B5) + 1.20
print ("B5:",round(B5,2))最後に、 x_B1、y_B1に格納した水素原子のx座標、y座標のうち、x軸の正方向、負方向、y軸の正方向、負方向の4方向を考えて、原点からの距離のもっとも遠い4点を抽出します。そのなかの最も小さいものをB1とします。以下を実行すると1.73という値が得られるかと思います。
#x軸、y軸正負それぞれ4方向のもっとも原点から離れている4点を代入するための変数
B1_minus_x = B1_minus_y = B1_plus_x = B1_plus_y = 0.0
for i in range(j):
#負の方向は、x_B1(y_B1)に格納されているi番目の値が、現在代入されている値より小さい場合、その値を代入
if x_B1[i] <= 0 and B1_minus_x > x_B1[i]:
B1_minus_x = x_B1[i]
if y_B1[i] <= 0 and B1_minus_y > y_B1[i]:
B1_minus_y = y_B1[i]
#正の方向は、x_B1(y_B1)に格納されているi番目の値が、現在代入されている値より大きい場合、その値を代入
if x_B1[i] > 0 and B1_plus_x < x_B1[i]:
B1_plus_x = x_B1[i]
if y_B1[i] > 0 and B1_plus_y < y_B1[i]:
B1_plus_y = y_B1[i]
#4点の原点からの距離のうち最大のものを抽出
B1 = min(-B1_minus_x, B1_plus_x, -B1_minus_y, B1_plus_y )+1.20
print("B1:",round(B1,2))
これをそれぞれの分子に対して実行していくか(上記の座標、原子名を読み込むところのxyzファイルのファイル名を変える)、あるいは上記を関数にして一気に実行します。関数とした対応するファイルはGitHub上にあげてあります(Sterimol_all.py)。
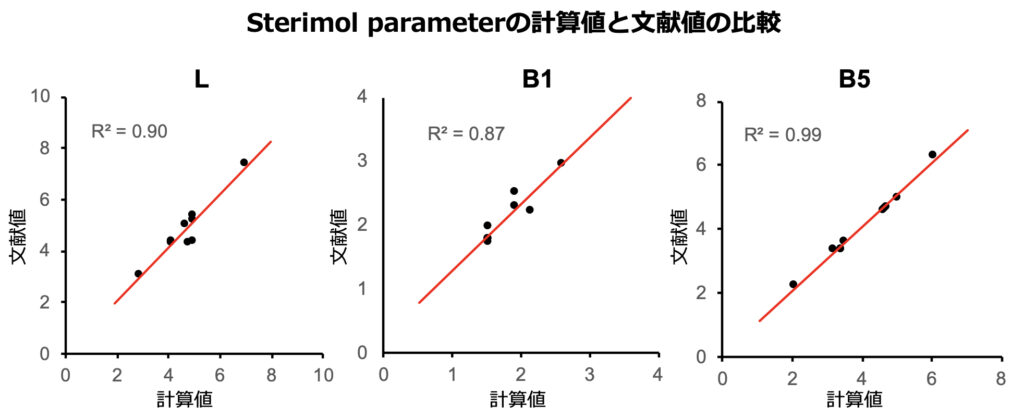
配座依存性はどうであるかなどいろいろと改善の余地がありそうですが、こうして算出したSterimol parameterの値を文献値と比較してみると、決定係数はすべて0.85以上となっています。とにかくSterimol parameterが算出できました。
では実際にSterimol parameterを使ってみましょう。記述子計算に使ったカルボン酸の構造は上述のようにTaft-Charton値を算出するのに使われたデータセットです。対応するカルボン酸のエステル化の反応速度定数が入手可能(JACS 1975, 97, 1552.)ですので、これを目的変数とし、算出したSterimol値を記述子として前回の記事のやり方で、重回帰モデルを作ってみます。Rのコードは以下になります。目的変数(反応速度定数:rate_constant.txt)および計算したSterimol parameterの値(Sterimol.txt)はGitHubにあげてあります。
#データの読み込み
rate_constant <- read.table("rate_constant.txt",row.names = 1)
Sterimol <- read.table("Sterimol.txt",row.names = 1)
#回帰分析
fit <- lm(as.matrix(rate_constant) ~., data = as.data.frame(Sterimol))
result <- step(fit, direction = "both")
summary(result)
#一つ抜き交差検証
vyploo = c()
for (i in 1:26){
cv_fit <- lm(as.matrix(rate_constant[-i,]) ~., data=Sterimol[-i,])
yploo <- predict(cv_fit,newdata=Sterimol[i,])
vyploo[i] <- yploo
}
q2 <- 1-sum((vyploo-rate_constant)**2)/sum((rate_constant-mean(as.matrix(rate_constant)))**2)
q2前回の記事で、テストセットの決定係数R2test > 0.6、一つ抜き交差検証から算出した決定係数q2 > 0.5がQSARにおける回帰モデルの評価基準のひとつであることを述べました。今回、上記を実行してみると訓練データから計算した決定係数が0.67(Summaryを実行した際のMultiple R-squaredの値)、一つ抜き交差検証から算出した決定係数は0.53ということでq2 > 0.5は満たすものの若干記述能が低いようにも見えます。実際、SigmanらはSterimol parameterではCH2tBu基とnPr基があまりみわけられていないことに言及しています(JACS 2014, 136, 5783.)。
上記のように、置換基の幅と長さからなる3次元の立体記述子であるSterimol parameterの記述能が、ある場合において高くないことに気づいた2013年当時、筆者は次のように考えました。
3次元では分子構造の記述能が高くない場合があるのならば分子構造をもっと"バラバラ"にしてしまえばよいのではないか、つまり分子をデジタル化してしまえばよいのではないか
すなわち下図のように分子を格子空間にいれて、単位格子に分子が含まれる場合はその単位格子を1、含まれない場合は0として記述子としてしまえばよいのではないかというアイデアです。

これが本サイトの主題である分子場解析の記述子である分子場のひとつ、Indicator fieldです。次回はIndicator fieldを算出するためのPythonのプログラムを見ていきます。 (2025.8.6追記) Indicator fieldを用いた分子場解析が可能な、データ駆動型触媒設計のための無料webアプリを大学・公的研究機関向けに公開しました。


コメント